Problem definition
In Gene Regulatory Networks (GRNs), regulator genes \( R \) interact with target genes \( T \) to control cellular processes. These interactions can be activating, when the regulator enhances the target’s expression, or repressing, when it decreases the expression. The regulatory relationships are directional, flowing from the regulator gene \( R \) to the target gene \( T \). We represent these relationships as directed edges \( \textbf{e}_{RT} \). The goal is to predict the type of regulation \( \textbf{r}_{RT} \) between regulator gene \( R \) and target gene \( T \), which can be activation, repression, or non-regulated.
Overview of the XATGRN
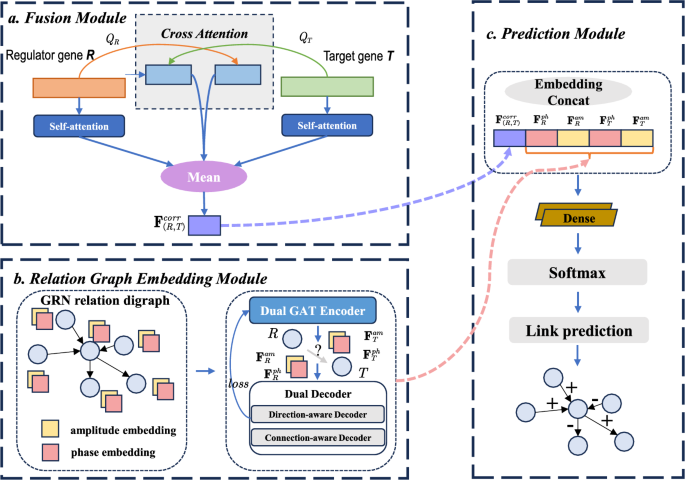
Overview of the XATGRN method
Our Cross-Attention Complex Dual Graph Embedding Model (XATGRN) is designed to infer the regulation types for Gene Regulatory Networks (GRNs). In particular, our XATGRN can distinguish between the activation type and repression type. Our model operates by treating the GRN inference problem as the link prediction task between regulator genes \( R \) and target genes \( T \). As shown in Fig. 1, our model extracts key features from both bulk gene expression data and existing databases that detail prior regulatory associations with regulation types, refining these features through a softmax classifier to predict the regulatory relationships as either activation, repression, or non-regulated interactions.
Initially, the gene expression profiles of regulator-target gene pairs \( (R, T) \) are used by the fusion module (Fig. 1a), yielding the fusion embedding vector. This vector encapsulates the gene expression features and the correlation information between the regulator and target genes. Subsequently, our Relation Graph Embedding Module The complex embeddings capture both the connectivity and directionality within the network.
Ultimately, the fusion embedding, along with the complex embeddings of regulator gene \( R \) and target gene \( T \), are concatenated to form a comprehensive feature set in the prediction module (Fig. 1c). This aggregated information is then fed into a softmax classifier for predicting the GRN relation.
Fusion module
Our Fusion Module extracts gene expression features from both the regulator gene \( R \) and the target gene \( T \). This module captures the interactions between the gene pair \( (R, T) \), which are essential for predicting regulatory mechanisms within gene regulatory networks (GRNs), as shown in Fig. 1a.
To address the shortcomings of conventional one-dimensional CNNs used by DeepFGRN [28], we introduce the Fusion Module. This module is based on the Cross-Attention Network (CAN), inspired by FusionDTI [31]. In particular, CAN enables our model to focus on the most relevant aspects of the gene expressions, which significantly improves its capacity to extract meaningful representations.
The gene expression data for the regulator gene \( R \) and the target gene \( T \) are processed to generate queries, keys, and values for the cross-attention mechanism, denoted as \( \textbf{Y}_R \) and \( \textbf{Y}_T \), respectively. The queries, keys, and values for gene \( R \) are represented as \( Q_R, K_R, V_R \) and for gene \( T \) as \( Q_T, K_T, V_T \). The projection matrices \( W_q^R, W_k^R, W_v^R \) and \( W_q^T, W_k^T, W_v^T \) map the gene data into the corresponding representations. Specifically, those matrices are defined as follows:
$$\begin{aligned} Q_R&= Y_R W_q^R,&K_R&= Y_R W_k^R,&V_R&= Y_R W_v^R, \end{aligned}$$
(1)
$$\begin{aligned} Q_T&= Y_T W_q^T,&K_T&= Y_T W_k^T,&V_T&= Y_T W_v^T. \end{aligned}$$
(2)
Multi-head self-attention and cross-attention mechanisms are subsequently applied. Notably, each gene retains half of its original self-attention embedding and half of its cross-attention embedding, which allows the model to better handle the intrinsic features of each gene while capturing the complex interactions between them. These embeddings encapsulate the intricate regulatory interactions, thereby enhancing our model’s capacity to discern the relationship between the genes.
The embeddings from both the regulator and target genes are then concatenated to form a combined embedding. Such a combined embedding is processed to produce the correlation embedding, which represents the regulatory relationship between the gene pair \( (R, T) \).
The fusion module and the subsequent steps are defined by the following equations:
$$\begin{aligned} R^* = \frac{1}{2}\left[ MHA\left( Q_R, K_R, V_R\right) + MHA\left( Q_T, K_R, V_R\right) \right], \end{aligned}$$
(3)
$$\begin{aligned} T^* = \frac{1}{2}\left[ MHA\left( Q_T, K_T, V_T\right) + MHA\left( Q_R, K_T, V_T\right) \right], \end{aligned}$$
(4)
$$\begin{aligned} \textbf{F}_{(R,T)}^{fusion} = \text {Concat}\left( \left( \text {MeanPool}(R^*), \text {MeanPool}(T^*)\right), 1\right), \end{aligned}$$
(5)
where the embeddings \( R^* \) and \( T^* \) represent the enhanced representations of the regulator and target genes, respectively. Specifically, \( R^* \) integrates information from both the regulator’s self-attention and the cross-attention with the target, while \( T^* \) integrates information from both the target’s self-attention and the cross-attention with the regulator. The mean pooling operation is denoted by \( \text {MeanPool} \), and the concatenation operation is denoted by \( \text {Concat} \). The final fusion embedding \( \textbf{F}_{(R,T)}^{fusion} \) represents the regulatory relationship between the regulator and target genes.
Relation graph embedding module
The Relation Graph Embedding Module addresses the complexity of representing nodes within Gene Regulatory Networks (GRNs). It handles the challenges posed by high-dimensional, sparse, and directed interactions. Specifically, it leverages the skewed degree of genes, which is crucial for differentiating between regulator and target nodes in GRNs.
To effectively embed the nodes in a GRN, we adopt the Complex Dual Graph Embedding approach from the DUPLEX framework [29]. As shown in Fig. 1b, this approach generates amplitude and phase embeddings for both regulator and target genes, which encode both the connectivity and directionality of the regulatory interactions.
We model a directed graph (digraph) \( G = (V, E) \), where \( V \) represents the nodes and \( E \) represents the directed edges. Each edge \( (R, T) \in E \) symbolizes a regulatory link from the regulator gene \( R \) to the target gene \( T \). Here, R and T are specific instances of genes u in the graph, where R acts as a regulator and T as a target in the regulatory relationship.Our objective is to map each gene \( u \) to a \( d \)-dimensional vector \( \textbf{x}_u \in \mathbb {C}^{d \times 1} \).
To represent the directionality and connectivity of edges in GRN, our XATGRN leverage the Hermitian Adjacency Matrix (HAM). This approach is particularly effective in addressing the challenge of asymmetric digraphs in GRNs. We use H to denote the HAM, which is defined in polar form as:
$$\begin{aligned} H = A_s \odot \exp \left( i \frac{\pi }{2} \Theta \right), \end{aligned}$$
(6)
where \( i \) is the imaginary unit and \( \odot \) represents the Hadamard product. The symmetric binary matrix \( A_s \) is defined as:
$$\begin{aligned} A_s(u, v) = {\left\{ \begin{array}{ll} 1 & \text {if } (u, v) \in E \text { or } (v, u) \in E, \\ 0 & \text {otherwise}. \end{array}\right. } \end{aligned}$$
(7)
The antisymmetric matrix \( \Theta \) contains elements from the set \( \{-1, 0, 1\} \) defined as:
$$\begin{aligned} \Theta (u, v) = {\left\{ \begin{array}{ll} 1 & \text {if } (u, v) \in E, \\ -1 & \text {if } (v, u) \in E, \\ 0 & \text {otherwise}. \end{array}\right. } \end{aligned}$$
(8)
Hence, the HAM’s entries \( H(u, v) \), taking values in the set \(\{i, -i, 1, 0\}\), effectively capture the relationships in GRNs, representing four different types of status between u and v including forward, reverse, bidirectional interactions and non-existing. This representation is particularly suited to GRNs, where regulatory interactions can be both directional and varied in nature. In contrast, the traditional asymmetric adjacency matrix \( A \) necessitates separate entries for \( A(u, v) \) and \( A(v, u) \), each restricted to \(\{0, 1\}\), to encode the same diversity of relationships. The HAM’s ability to integrate directionality and connectivity in a single, symmetric matrix offers a more comprehensive and efficient representation, aligning perfectly with the intricate patterns observed in GRNs.
Furthermore, the matrix decomposition \( H = X^{\top } \overline{X} \), where \( X \) is the node embedding matrix, represents the inner product between \( X \) and its complex conjugate \( \overline{X} \). This decomposition facilitates the expression of the node embedding \( \textbf{x}_u \) in polar form. Specifically, the embedding is written as follows:
$$\begin{aligned} \textbf{x}_u&= a_u \odot \exp \left( i \frac{\pi }{2} \theta _u\right), \end{aligned}$$
(9)
$$\begin{aligned} \overline{\textbf{x}}_u&= a_u \odot \exp \left( -i \frac{\pi }{2} \theta _u\right). \end{aligned}$$
(10)
where \( a_u \) represents the amplitude and \( \theta _u \) the phase of the embedding \( \textbf{x}_u \). These complex conjugate embeddings \( \textbf{x}_u \) and \( \overline{\textbf{x}}_u \) are interpreted as the representations of the regulator and target roles of gene node \( u \), respectively. This joint embedding strategy, in contrast to using separate embeddings for the regulator and target, enables co-optimized learning from both the incoming and outgoing edges of the node \( u \). Such an approach effectively addresses the challenge of the imbalance between in-degrees and out-degrees, which can significantly affect the embedding quality of nodes within Gene Regulatory Networks (GRNs).
Dual GAT Encoder
Based on HAM, we will introduce a dual encoder architecture that comprises an amplitude encoder, a phase encoder, and a fusion layer. The encoders refine node embeddings by aggregating information from both incoming and outgoing edges of node\( u \), effectively addressing the issue of skewed degree distribution.
The amplitude encoder employs GAT to aggregate information from both incoming and outgoing edges for each node. This process captures the node’s overall connectivity, ensuring that even nodes with varying in-degrees and out-degrees are embedded with high quality in the context of the network’s topology:
$$\begin{aligned} \textbf{a}_{u}^{\prime } = \text {ReLU}\left( \sum _{v \in \mathcal {N}(u)} \alpha _{uv}^{(am)} \cdot \textbf{a}_{v} \right), \end{aligned}$$
(11)
where \(\mathcal {N}(u)\) denotes the set of neighboring nodes connected to node u via either incoming or outgoing edges, \( \alpha _{uv}^{(am)} \) is the attention coefficient for amplitude embedding, and \( \textbf{a}_{u}^{\prime } \) represents the updated amplitude embedding for node \( u \).
The phase encoder captures the directionality of regulatory relationships by distinguishing between nodes acting as regulators and targets. The phase embedding is updated similarly using a direction-sensitive attention mechanism:
$$\begin{aligned} \theta _u’ = \text {ReLU} \left( \sum _{v \in \mathcal {N}_{\text {in}}(u)} \alpha _{uv}^{(ph)} \cdot \theta _v – \sum _{v \in \mathcal {N}_{\text {out}}(u)} \alpha _{uv}^{(ph)} \cdot \theta _v \right), \end{aligned}$$
(12)
where \(\mathcal {N}_{\text {in}}(u)\) and \(\mathcal {N}_{\text {out}}(u)\) denote the sets of in-neighbors and out-neighbors of node u, respectively, and \(\alpha _{uv}^{(ph)}\) is the attention coefficient for phase embeddings.
The refined embeddings \(\theta _u’\) and \(\textbf{a}_{u}^{\prime }\) from each layer become the input features for the next graph attention layer, allowing hierarchical abstraction of regulatory patterns.
The fusion layer is a critical component that combines the amplitude and phase embeddings, which carry distinct yet complementary information. This layer ensures that the embeddings from both encoders are effectively integrated to capture the comprehensive regulatory interactions within the GRN. The fusion process is designed to balance the contributions from both the amplitude and phase embeddings, thereby enhancing the model’s ability to represent complex gene interactions accurately.
The fusion layer operates by combining the information from the amplitude and phase embeddings at each layer of the encoder. This is achieved through differentiated aggregation mechanisms where amplitude fusion preserves undirected connectivity while phase fusion maintains directional relationships: For amplitude embeddings:
$$\begin{aligned} \textbf{F}_u^{am} = \text {ReLU}\left( \sum _{v \in \mathcal {N}(u)} \alpha _{uv}^{(am)} \cdot \textbf{a}_{v} + \sum _{v \in \mathcal {N}(u)} \alpha _{uv}^{(ph)} \cdot \mathbf {\theta }_{v} \right), \end{aligned}$$
(13)
where \(\textbf{F}_u^{am}\) represents the updated amplitude embedding for node \(u\), \(\alpha _{uv}^{(am)}\) and \(\alpha _{uv}^{(ph)}\) are the attention coefficients for amplitude and phase embeddings, respectively.
For the phase embeddings, it applies a directional aggregation operator for fusion of the phase embedding:
$$\begin{aligned} \textbf{F}_u^{ph} = \text {ReLU}\left( \oplus \{\theta _v\} + \oplus \{\textbf{a}_v\} \right) \end{aligned}$$
(14)
where \(\textbf{F}_u^{ph}\) represents the updated phase embedding for node \(u\) and the directional aggregation operator \(\oplus \) is defined as:
$$\begin{aligned} \oplus \{x_v\} \triangleq \sum _{v \in \mathcal {N}_{\text {in}}(u)} \alpha _{uv}^{(ph)} \cdot x_v – \sum _{v \in \mathcal {N}_{\text {out}}(u)} \alpha _{uv}^{(ph)} \cdot x_v \end{aligned}$$
(15)
These updated embeddings, \(\textbf{a}_{u}^{\prime }\) and \(\mathbf {\theta }_{u}^{\prime }\), are then propagated to the subsequent layers in their respective encoders. The fusion layer ensures that the information from both the amplitude and phase embeddings is effectively utilized in the following steps.
Dual Decoders and Loss Functions
After obtaining the embedding features for each gene node, we introduce 2 parameter-free decoders to reconstruct the Hermitian Adjacency Matrix (HAM). These decoders are designed to ensure that the embeddings capture both the connectivity and directionality of the regulatory interactions within the GRN.
The HAM reconstruction process explicitly preserves four edge types in \(\mathcal {R} = \{i, -i, 1, 0\}\), corresponding to forward, reverse, bidirectional, and non-existent regulatory relationships. Our dual decoding strategy separates directional semantics from topological connectivity through specialized modules:
The direction-aware decoder aims to reconstruct the directionality of regulatory interactions. This task is formulated as a classification problem in GRN, where each edge \( (u, v) \) is assigned probabilities that correspond to its edge type (forward, reverse, bidirectional, or no edge). The predicted edge type is determined by the minimum distance between the estimated matrix element \( \hat{H}(u, v) \) and the possible edge types r:
$$\begin{aligned} \text {pred. type} = \underset{r}{\text {argmin}} \left( \text {Dist}(\hat{H}(u, v), r) \right),\quad \forall r \in \mathcal {R}, \end{aligned}$$
(16)
where \( \text {Dist}(\hat{H}(u, v), r) \) is the distance between \( \hat{H}(u, v) \) and r.
The probabilities \( P(\hat{H}(u, v) = r) \) are calculated as follows:
$$\begin{aligned} P(\hat{H}(u, v) = r) = \frac{\exp (-|\textbf{x}_u^{\top } \overline{\textbf{x}}_v – r|)}{\sum _{r’ \in \mathcal {R}} \exp (-|\textbf{x}_u^{\top } \overline{\textbf{x}}_v – r’|)}, \quad \forall r \in \mathcal {R}. \end{aligned}$$
(17)
The self-supervised direction-aware loss is then defined as:
$$\begin{aligned} \mathcal {L}_d = -\sum _{r \in \mathcal {R}} \sum _{H(u, v) = r} \log P(\hat{H}(u, v) = r). \end{aligned}$$
(18)
The connection-aware decoder is designed to reconstruct the binary presence of connections between genes, which reconstruct \(A_s\)—the amplitude component of the HAM defined in Eq. 6. It models the connection probability for an edge \( (u, v) \) as:
$$\begin{aligned} P(\hat{A}_s(u, v) = 1) = \sigma (a_u^{\top } a_v), \end{aligned}$$
(19)
where \( \sigma \) is the sigmoid function and \( \hat{A}_s \) is the estimated amplitude component of the HAM representing the probability that a connection exists between genes u and v. The connection-aware loss function \( \mathcal {L}_c \) adheres to the same negative log-likelihood minimization principle as the direction-aware loss:
$$\begin{aligned} \mathcal {L}_c = -\sum _{u, v} \log P(\hat{A}_s(u, v) = Atwo sta_s(u, v)). \end{aligned}$$
(20)
Total Loss
The total loss function combines the direction-aware and connection-aware losses to ensure that the model learns both the connectivity and directionality of the regulatory interactions. The total loss is given by:
$$\begin{aligned} \mathcal {L}_{total} = \mathcal {L}_d + \lambda _k \mathcal {L}_c, \end{aligned}$$
(21)
where the connection-aware weight \(\lambda _k = \lambda _0 q^k\) dynamically evolves with training epoch k, starting from initial value \(\lambda _0\) and decaying via decay rate \(q<1\).
By leveraging the fusion module and the Relation Graph Embedding Module, our XATGRN can effectively capture the connectivity and directionality of regulatory interactions within the network and alleviate the issue due to skewed degree distribution in GRNs.
Prediction module
The prediction module in our model is designed to leverage the embeddings generated by the Fusion Module and the Relation Graph Embedding Module to make accurate predictions about the regulatory relationships within the Gene Regulatory Network (GRN). As shown in Fig. 1c, this module integrates the complex embeddings of genes and employs a series of neural network layers to classify the interactions between gene pairs (R, T).
For each sample, the module processes the feature and label data for a gene pair (R, T), where R is the regulator gene and T is the target gene. The features from the Fusion Module are denoted as \( \textbf{F}_{(R,T)}^{fusion} \), while the features from the Relation Graph Embedding Module includes the amplitude and phase embeddings for both genes: \( \textbf{F}_R^{am} \), \( \textbf{F}_T^{am} \), \( \textbf{F}_R^{ph} \), and \( \textbf{F}_T^{ph} \).
These embeddings are concatenated to form a comprehensive feature vector:
$$\begin{aligned} \textbf{F}&= \text {concat}(\textbf{F}_{(R,T)}^{fusion}, \textbf{F}_R^{am}, \textbf{F}_T^{am}, \textbf{F}_R^{ph}, \textbf{F}_T^{ph}). \end{aligned}$$
(22)
The concatenated feature vector \(\textbf{F}\) is first processed through a 1-dimensional convolutional layer with batch normalization (BN) and max pooling, followed by ReLU activation to extract and refine spatial features:
$$\begin{aligned} x_1&= \text {ReLU}(\text {MaxPool}(\text {BN}(\text {Conv1D}(\textbf{F})))), \end{aligned}$$
(23)
where the output is \( x_1 \), and the vector \( x_1 \) is pass to the global average pooling layer:
$$\begin{aligned} x_2&= \text {GlobalAvgPool}(x_1), \end{aligned}$$
(24)
where the resulting vector is denoted as \( x_2 \).This step condenses the feature map into a fixed-size vector that captures the essential information for classification.
Subsequently, the flattened vector \( x_2 \) is passed through two fully connected layers(\(\text {FC}_1\) and \(\text {FC}_2\)) with dropout for regularization, where a dropout rate of \(p=0.3\) is applied:
$$\begin{aligned} x_3&= \text {FC}_2(\text {Dropout}(\text {ReLU}(\text {FC}_1(x_2)), p=0.3)), \end{aligned}$$
(25)
where \(x_3\) represents the output of the second fully connected layer, and \(x_3\) is then passed through a softmax function to produce the final classification probabilities over C classes:
$$\begin{aligned} \text {output}&= \text {softmax}(x_3) \end{aligned}$$
(26)
To address class imbalance, we employ a weighted cross-entropy loss function \(\mathcal {L}\). The weights \(w_c\) for each class \(c\) are inversely proportional to their frequency in the dataset:
$$\begin{aligned} w_c&= \frac{N_{\text {total}}}{N_c}, \end{aligned}$$
(27)
where \(N_{\text {total}}\) is the total number of samples in the dataset, and \(N_c\) is the number of samples in class \(c\).
The loss function \(\mathcal {L}\) is then defined as:
$$\begin{aligned} \mathcal {L}&= -\sum _{c=1}^{C} w_c \cdot y_c \cdot \log (\hat{y}_c), \end{aligned}$$
(28)
where \(y_c\) is the true label for class \(c\), and \(\hat{y}_c\) is the predicted probability for class \(c\).
Our model optimizes this loss function using the Adam optimizer, with an exponential learning rate scheduler to ensure stable and efficient convergence.
Model inference
The XATGRN inference workflow for new datasets comprises three key phases: Given N genes \(\{g_1,…,g_N\}\), we enumerate all possible directed regulatory pairs \((g_i, g_j)\) with \(i \ne j\). This produces \(N(N-1)\) candidate relationships that form the prediction space.
Each candidate pair is processed through the trained XATGRN model to estimate regulatory probability \(P_{ij}\). The dual-module architecture ensures simultaneous evaluation of both connection existence (\(\mathcal {L}_c\)) and interaction type (\(\mathcal {L}_d\)). A probability threshold \(\tau \) is applied to generate the final adjacency matrix:
$$\begin{aligned} A_{ij} = \mathbb {I}(P_{ij} \ge \tau ) \end{aligned}$$
(29)
where \(\mathbb {I}\) is the indicator function. The default \(\tau =0.8\) was established through validation on holdout biological datasets.