Nomenclature
In this work, we used the terms “brain region” in a broad sense: it might label entire regions (thalamus, cerebellum), sub-regions (primary, secondary motor areas), or layers separation (primary motor area, layer 5, layer 6).
We used brain regions acronyms defined in the Allen Brain Atlas37. We spelled out each acronym that is helpful for this work’s comprehension when they were used. We also provided an exhaustive list of all brain acronyms used in the Supplementary section 10.1.
Long-range axon synthesis
We presented an algorithm for synthesizing LRAs in ref. 23. This method was able to synthesize cells accurately mimicking reconstructed axonal morphologies. We review here the main relevant steps of this algorithm; see Fig. 6. Reconstructed axonal morphologies are taken as input. Terminations that are close together (within a radial and path distance) are clustered up to their common ancestors in so-called tufts. The axons with all tufts taken out are labeled as trunks. The somata of the reconstructed morphologies are used as source points, and the locations of the tufts ancestors as target points. A graph is created with these and additional points taken as vertices (see ref. 23 for details). Then, we run the weighted Steiner tree algorithm38 on this graph, which connects the targets while minimizing cable length, and allowing to prefer edges, such as ones that would be inside fiber tracts. The created trunk is then post-processed to reproduce local morphometrics of biological axons, with operations such as adding random noise and taking into account local history for modifying the curvature. Finally, the tufts that were initially clustered are synthesized based on their topological properties, with the method previously described and validated for synthesizing dendritic morphologies8.
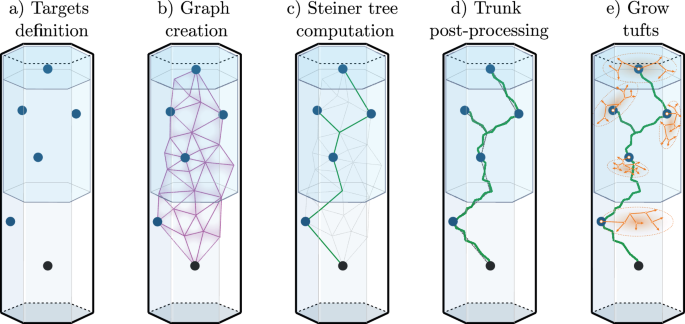
From an input biological axon, we take the soma as the source point (a), cluster the tufts, and make their common ancestors the target points. The synthetic trunk is created by connecting the targets from the source point with the Steiner tree on a graph method (b, c). The trunk is then post-processed (d) with the addition of noise to reproduce local morphometrics of biological axons. Finally, the tufts are grown (e) at the target points from their topological properties, with the same method as dendrites8.
We could assess that this algorithm was able to produce morphometrical properties that matched with the reconstructed axons at the trunk, tuft, and morphology levels, see ref. 23.
Axonal projections analysis
In our previous work23, the source points and the target points were taken directly as the somata and common ancestors of tufts of the reconstructed morphologies, respectively. Furthermore, the topological signature of the tufts of the biological axon to mimic was used for their synthesized analogs. In the present work, we generalized the selection of source points, target points, and tufts from populations of biological axons rather than from individual morphologies. This eventually allowed us to synthesize and connect neurons in the entire mouse brain, within and between brain regions.
We explain our methodology in what follows, see Fig. 7 for a visual schematic.
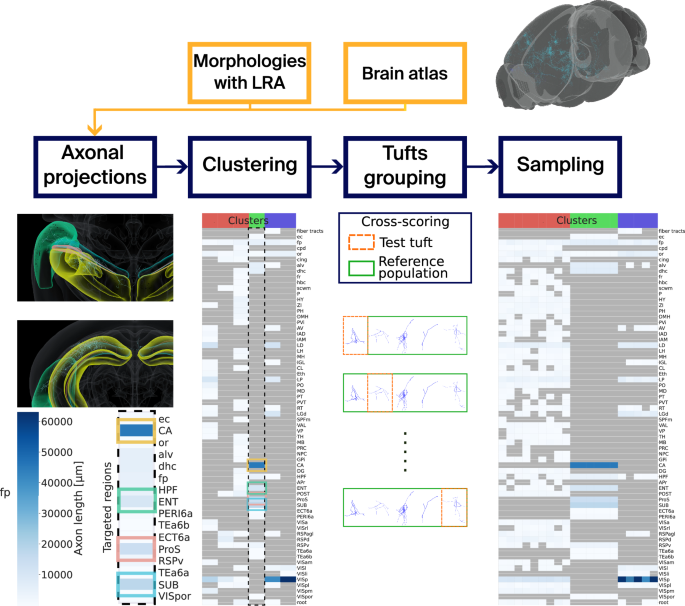
Neuronal morphologies with long-range axons (LRAs) placed in a mouse brain atlas are taken as input. The projections of the LRAs are computed, and we cluster the LRAs based on these projections with GMMs. Tufts are separated from the trunks of the LRAs, and they are counted and assigned a score for each cluster and target brain region. Finally, we can use the GMMs to sample target axon lengths for every target brain region defined in the clusters. fp: corpus callosum, posterior forceps.
Input data
Morphologies
We used morphologies with long-range axons from three different sources:
-
1084 morphologies from the Janelia MouseLight Project25.
-
1741 morphologies from ref. 24.
-
800 unpublished morphologies from collaboration with Southeast University, Nanjing, China and H. Peng (using the same protocol as ref. 24).
For the latter set unpublished morphologies, the protocol used was the same as ref. 24. In other words, we used transgenic mice that contain a combination of the following individual driver and reporter lines: Cux2-CreERT2, Fezf2-CreER, Gnb4-IRES2-CreERT2, Plxnd1-CreER, Pvalb-T2A-CreERT2, Tnnt1-IRES2-CreERT2, Vipr2-IRES2-Cre-neo, Snap25-IRES2-Cre, Slc17a7IRES2-Cre, Esr2-IRES2-Cre, Ai139, Ai140, Ai82, Ai166, Ai14, Ai65F, and RCL-Sun1sfGFP. All transgenic mice were maintained in C57BL/6J congenic background. For each genotype of transgenic mice, we used both male and female mice, ages ranging from 8 weeks to 5 months old. Mice were housed in animal rooms on a 14/10 h light/dark cycle (6 am–8 pm light). The room temperature was set at 70 ∘F (21 ∘C) and the relative humidity at 40%. The study did not involve wild animals. All experimental procedures using live animals were performed according to protocols approved by Institutional Animal Care and Use Committee (IACUC) of the Allen Institute for Brain Science.
Morphologies could be incompatible with our methodology for reasons such as incomplete reconstructions or artifacts due to the reconstruction techniques. Therefore, we post-processed them with the Repair workflow of Morphology-Workflows software39, which applied corrections such as repairing out-of-plane cut branches or removing unifurcations. 16 (8 from ref. 25 + 8 from ref. 24) morphologies did not pass all the correcting processes, and 8 (1 + 5 + 2) did not pass the axonal projection analysis (due to being detected out of bounds or having faulty axons). In total, 3601 morphologies were used in this work.
Mouse brain atlas
We used the mouse brain atlas described in ref. 29, which is an enhancement of the Common Coordinate Framework version 3 (CCFv3) atlas of the Allen Brain Institute37. Notable additions are the annotations of the barrel field areas and the distinction of cortical layers 2 and 3.
Projections computation
In order to generalize the axon synthesis algorithm, we first computed the projections of reconstructed biological axons by counting the number of terminals of each axon in all regions they terminated and computing the axon path lengths in these regions. Our method then uses one of these features to cluster the axons with somata in the same source region.
Let us formalize this problem in the following way. We want to classify a set of N biological neurons. Let a be the axon of a neuron n. We denote sa as the source brain region where the soma of neuron n is located. The axon a projects and terminates in a number of target brain regions, \({t}_{a}\in {({\mathbb{N}})}^{B}\) is the vector counting the number of terminal points in all brain regions B. In other words, \({t}_{a}^{(b)}\) is the number of terminal points of axon a into brain region b. We define in a similar way \({l}_{a}\in {({{\mathbb{R}}}^{0+})}^{B}\) the path length of axon a inside brain region b. Note that brain regions can be defined at various levels of detail according to the hierarchy of the brain atlas. Let us further denote fa, the feature vector for the classification of neuron a. We consider the case where fa = la. sa is not included in fa because we impose a separate classification for each source region.
Clustering method
There are several methods for unsupervised clustering of data such as K-means and its variants (K-medoids, K-centroids40) and hierarchical clustering based on statistical difference of the subclasses28. We chose here to assume that our data could be described by normal probability density functions, using GMMs41. Let us imagine that region sa has \(C\in {\mathbb{N}}\) clusters. To assume that a originates from a GMM is equivalent to saying that the probability of a to belong to cluster c is given by :
$$P(c| a)=\frac{P(c)P(a| c)}{P(a)}$$
(2)
$$=\frac{{p}_{c}{{{\mathcal{N}}}}({f}_{a},{\mu }_{c},{\Sigma }_{c})}{{\sum }_{k=1}^{C}{p}_{k}{{{\mathcal{N}}}}({f}_{a},{\mu }_{k},{\Sigma }_{k})},$$
(3)
where \({{{\mathcal{N}}}}({f}_{a},{\mu }_{c},{\Sigma }_{c})\) is the multivariate normal distribution with mean μc and covariance matrix Σc:
$${{{\mathcal{N}}}}({t}_{a},{\mu }_{c},{\Sigma }_{c})=\frac{1}{\sqrt{{\left(2\pi \right)}^{B}\det ({\Sigma }_{c})}}\exp \left(-\frac{1}{2}{\left({f}_{a}-{\mu }_{c}\right)}^{T}{\Sigma }_{c}^{-1}({f}_{a}-{\mu }_{c})\right).$$
(4)
We assume Σc symmetric and positive definite ∀c ∈ C. Note that we have the constraint \({\sum }_{k=1}^{C}{p}_{k}=1\).
A common technique42 to optimize the clustering is to maximize the likelihood, or log-likelihood, of the observed data, based on the parameters of clustering θ42. Here, we can write θ = {p1, . . . , pC, μ1, . . . , μC, Σ1, . . . , ΣC}. The log-likelihood of the data based on the parameters of clustering is given by (assuming a are iid) :
$$l(\theta )=\log \left(\mathop{\prod }_{a=1}^{N}P(a)\right)=\log \left({\prod }_{a=1}^{N}{\sum }_{k=1}^{C}{p}_{k}{{{\mathcal{N}}}}({f}_{a},{\mu }_{k},{\Sigma }_{k})\right):=\log \left({\prod }_{a=1}^{N}P({f}_{a}| \theta )\right).$$
(5)
However, optimizing the log-likelihood (5) is not tractable in the case of large GMMs. Instead, we used the Expectation-Maximization (EM), see Supplementary Material 10.2.1.
The number of clusters C for a source region can be either imposed or selected to maximize a score, the BIC, see Supplementary Material 10.2.2. Since we were less interested in describing the biological data in this work than reproducing it, the number of clusters C per source region s is optimized on the BIC score within a range of C going from the number of axons Ns in s divided by 2, to Ns, unless specified otherwise.
Tufts grouping
Once the GMM clusters were defined for all source regions of the input axons, the tufts were clustered using the previously described clustering algorithm, section “Long-range axon synthesis” and ref. 23. We used a maximum clustering radius and path distance of 300 μm. The tufts were then grouped by GMM cluster and region of their common ancestors. For each group g, we computed the average \({\bar{N}}_{{{{\rm{tufts}}}}}^{(g)}\) and variance \({\sigma }^{2}({N}_{{{{\rm{tufts}}}}}^{(g)})\) of tuft numbers for each group. Finally, the tufts were assigned a representativity score within their group, which is a measure of how close they are to the other tufts in their group in terms of a set of morphometrical features. In this work, all morphometrics were computed using NeuroM43. We used the MVS score to measure the similarity of the features. The calculation details can be found in Supplementary Material 10.3.
Sampling
Finally, one can draw samples from the GMMs to verify the clustering. To do so, we first chose one distribution (or cluster c) from the mixture, our choice weighted by the probability pc. It is then possible to generate the vector of lengths la or terminal points ta by drawing a sample from the chosen distribution:
$${l}_{a} \sim {{{\mathcal{N}}}}({\mu }_{c},{\Sigma }_{c}).$$
(6)
We added a post-processing step to all samples, which removes values sampled in regions not observed in the biological input data.
We used the sampling here as an indicator of the clustering accuracy only. However, one could use the sampling to synthesize directly axons with the sampled lengths, for instance by choosing tufts to add up to all lengths in each targeted region.
Synthesizing in the mouse brain
We now present how we used the axonal projections analysis presented in section “Axonal projections analysis” as input data for the synthesis algorithm in section “Long-range axon synthesis” to synthesize LRAs in the mouse brain.
Initial morphologies synthesis
First of all, we synthesized neuronal morphologies made of somata, dendrites, and grafted reconstructed local axons in the isocortex, with the same methodology as in refs. 8,44. These local axons were copied from previous experimental reconstructions and grafted to the synthesized cells. Since mostly pyramidal cells of the mouse cortex project to distal regions45, we filtered pyramidal cells of the brain region sa and would replace their local axon with a synthesized LRA. We synthesized LRAs for all pyramidal cells in the regions for which we synthesize, but that can be changed to a provided portion of them.
Source points
The somata of the filtered pyramidal cells were used as the source points of the synthesis algorithm. We assigned a GMM cluster for each source point by randomly picking a cluster c with probability pc from the clusters C of source sa.
Target points
We computed the probability of an axon to target a brain region b as the number of axons targeting b, divided by the total number of axons in the cluster. For a picked target brain region, a number \({T}_{a}^{(b)} \sim {{{\mathcal{N}}}}\left({\bar{N}}_{{{{\rm{tufts}}}}}^{(g)},\sigma ({N}_{{{{\rm{tufts}}}}}^{(g)})\right)\) of target points were randomly placed inside b. All the targets of axon a were then connected with a better edge weight for targets inside fiber tracts to form the trunk. In this way, the trunk would preferentially follow the fiber tracts.
Tufts selection
Finally, tufts were selected for each target point with probability computed based on the representativity scores of their group g, and then synthesized with the NeuroTS software8.
Creating connections
Once all the morphologies were fully synthesized, we made axo-dendritic connections as described in ref. 2. In a few words, touches were detected based on the physical proximity of neurite branches and filtered based on a minimum inter-bouton interval. Touches were then pruned based on physiological synapse density and converted into synapses. Connections and connectivity matrices were analyzed using the ConnectomeUtilities software46.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.