Datasets
The proposed model was trained and tested using four public datasets: Davis, E, GPCR, and IC. The Davis dataset [26] includes selectivity measurements of kinase proteins and their associated inhibitors, along with their dissociation constants \(K_d\) ranging from 0.016 to 10,000. This reflects the affinity between drug molecules and target proteins, where a smaller \(K_d\) indicates stronger affinity, and a \(K_d\) of 10,000 or greater represents no significant association. Due to the large variance in \(K_d\) values within the Davis dataset, these values were log-transformed as follows:
$$\begin{aligned} \textbf{p}\textbf{K}_{\textbf{d}} = – {\mathbf{\log }\left( \frac{\textbf{K}_{\textbf{d}}}{10^{9}} \right) } \end{aligned}$$
(1)
Based on earlier work by Davis et al. [26], we set the threshold at 5.0, considering drug–target pairs with a value less than 5.0 as positive examples and the rest as negative examples, to construct a binary classification dataset. The datasets E, GPCR, and IC were sourced from the article by Bian et al. [23], which categorizes target proteins into three main types: Enzyme (E), G-Protein Coupled Receptor (GPCR), and Ion Channel (IC). Enzymes and Ion Channels are sourced from KEGG BRITE [27], DrugBank [28], SuperTarget [29], and BRENDA databases [30], while GPCRs are from the GLASS database [31].
Considering all DTIs in the dataset as positive examples and the rest as negative examples, the relevant data distribution is shown in Table 1.
Methods
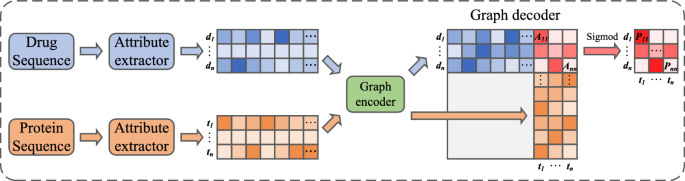
The overall architecture of the proposed SaeGraphDTI model is shown in Fig. 1. This model can be divided into three main components: the sequence attribute extractor, the graph encoder, and the graph decoder. First, the initial sequences of the drug and target are input into the sequence attribute extractor to obtain feature sequences with consistent lengths and aligned attributes. Next, the drug and target feature sequences are input into the graph encoder, which generates feature representations based on topological information. Finally, these are passed into the graph decoder to calculate the likelihood of a specific drug–target edge existing, thereby inferring potential DTIs.
Sequence attribute extractor
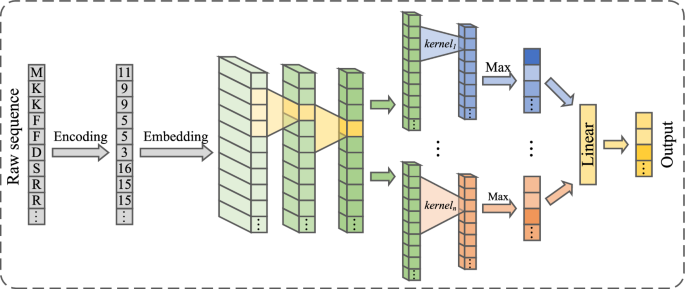
Drugs and targets are represented in the form of sequences, and their lengths are unified. The sequence attribute extractor, based on one-dimensional convolution with variable convolution kernels, captures the most salient outputs of the sequence under different convolution kernels, while maintaining the output order for each kernel. This ensures that the output of each sequence is an attribute list with aligned positions, as shown in Fig. 2. The outputs of the sequence attribute extractor for both drugs and targets are set to the same dimension to facilitate the subsequent processing by the graph encoder and decoder.
Structure of sequence attribute extractor
Embedding Layer
Appropriate representation methods can enable the model to capture more accurate information. Therefore, we use SMILES (Simplified Molecular Input Line Entry System) [32] strings as the serialized representation for drugs and amino acid sequences as the serialized representation for target proteins.
First, each element in the raw drug sequence and the raw target sequence is encoded so that the raw sequences can be represented as encoded sequences. For drug encoding, integers from 1 to 32 are used, while for target encoding, integers from 1 to 22 are used. Then, by either padding with zeros at the end or trimming the terminal sequences, the lengths of all drug or target encoded sequences are made consistent. Finally, the fixed-length encoded sequences are input into an embedding layer to generate the corresponding drug embedding matrix \(D_{embed} \in R^{L_{d} \times {Dim}_{d}}\) and target embedding matrix \(T_{embed} \in R^{L_{t} \times {Dim}_{t}}\), where \(L_{d}\) is the length of the drug sequence, \(L_{t}\) is the length of the target sequence, \( Dim_{d}\) is the embedding dimension for drugs, and \(Dim_{t}\) is the embedding dimension for targets.
Variable convolutional layer
CNNs can extract local features by moving convolutional kernels of fixed size over images or sequences, with the kernel size determining the receptive field of the convolution layer. To provide a broader initial receptive field for the sequence attribute extractor, after embedding the sequences, two CNNs with fixed-size kernels are first used for local feature extraction, each followed by an average pooling layer and a ReLU activation function layer. Then, multiple CNNs with different kernel sizes but consistent output channel numbers are employed. To capture the most prominent feature for each channel at the current kernel size, the maximum value from the convolution results is used as the output. The outputs from all convolution kernels are then concatenated into a one-dimensional tensor of length \(N_{kernel\_ size}{\times N}_{out\_ channel}\), where \(N_{kernel\_ size}\) is the number of kernel sizes and \(N_{out\_ channel}\) is the number of channels. Finally, this tensor is input into a fully connected (FC) layer, producing a one-dimensional feature vector of length \(N_{out\_ channel}\) for each original sequence.
This attribute extractor structure converts outputs of different dimensions with varying kernel sizes into outputs of the same dimension, resulting in one-dimensional feature sequences of consistent length as the final output of the sequence attribute extractor. By taking the maximum values at different kernel sizes, it captures the most suitable kernel size for each position, thereby identifying key subsequences of appropriate length that are most relevant to the results. This also ensures that our model does not incur significant loss when handling longer sequences, as we focus only on the most important parts.
Network construction
The original dataset is represented as a D–T (Drug–Target) network, where drugs and targets form all the nodes, and drug–target combinations with existing DTI (Drug–Target Interactions) constitute all the edges. By constructing D–D (Drug–Drug) and T–T (Target–Target) networks based on topology similarity calculation methods and combining them with the existing D–T network, a D–D–T–T (Drug–Drug–Target–Target) network that covers all drugs and targets can be built. Each node in the network can be connected to the remaining nodes through transitions, and the distance between nodes is represented by the number of transitions between them. The newly constructed edges reduce the number of transitions required between nodes and mitigate the loss of node information caused by frequent transitions, thereby alleviating the impact of the imbalanced dataset.
The graph encoder module, based on this network, uses graph neural network methods to propagate and update node information, thus incorporating topological information into the nodes. The graph decoder takes the node features encoded by the encoder and computes the probability of an edge existing between specific nodes, with drug–target pairs having higher probabilities considered as positive cases.
The set of all drugs is represented as \(D = \left\{ d_{1},d_{2},\ldots,d_{m} \right\} \), the set of all targets is represented as \(T = \left\{ t_{1},t_{2},\ldots,t_{n} \right\} \), the set of all drug–target interaction pairs is represented as E, where m is the number of drugs and n is the number of targets. If drugs and targets are treated as nodes and their interactions as edges, these nodes and edges form a drug–target interaction network, which can be represented by an interaction matrix A, as shown below:
$$\begin{aligned} \textbf{A}\left[{\textbf{d}_{\textbf{i}},\textbf{t}_{\textbf{j}}} \right]= \left\{ \begin{matrix} 1,& \quad if\,\left( {\textbf{d}_{\textbf{i}},\textbf{t}_{\textbf{j}}} \right) \in E \\ 0, & \quad otherwise \end{matrix} \right. \end{aligned}$$
(2)
The construction of the Drug–Drug approximate network and the Target–Target approximate network is based on the calculation of existing drug–target interaction pairs, including all interaction pairs in the calculation could result in the model’s performance being artificially inflated compared to the actual real-world performance. Therefore, the set of drug–target interaction pairs involved in constructing the approximate network is defined as B, with the number of elements in B being less than the total number of interaction pairs in A.
The similarity matrix between different drugs is defined as DS, and the calculation method for DS is as follows:
$$\begin{aligned} \textbf{D}\textbf{S}\left[\textbf{d}_{\textbf{i}},\textbf{d}_{\textbf{j}} \right]= \frac{1 + \textbf{D}\textbf{R}\left( {\textbf{d}_{\textbf{i}},\textbf{d}_{\textbf{j}}} \right) }{2} \cdot \frac{1 + \textbf{D}\textbf{C}\left( {\textbf{d}_{\textbf{i}},\textbf{d}_{\textbf{j}}} \right) }{2} \end{aligned}$$
(3)
Where DR is the Pearson similarity [33] and DC is the cosine similarity [34], calculated as follows:
$$\begin{aligned} & \textbf{D}\textbf{R}\left( {\textbf{d}_{\textbf{i}},\textbf{d}_{\textbf{j}}} \right) = \frac{\sum \limits _{\textbf{a} = 1}^{\textbf{n}}{\left( {\textbf{d}_{\textbf{i},\textbf{a}} – \overset{-}{\textbf{d}_{\textbf{i}}}} \right) \cdot \left( {\textbf{d}_{\textbf{j},\textbf{a}} – \overset{-}{\textbf{d}_{\textbf{j}}}} \right) }}{\sqrt{{\sum \limits _{\textbf{a} = 1}^{\textbf{n}}\left( {\textbf{d}_{\textbf{i},\textbf{a}} – \overset{-}{\textbf{d}_{\textbf{i}}}} \right) ^{2}} \cdot {\sum \limits _{\textbf{a} = 1}^{\textbf{n}}\left( {\textbf{d}_{\textbf{j},\textbf{a}} – \overset{-}{\textbf{d}_{\textbf{j}}}} \right) ^{2}}}} \end{aligned}$$
(4)
$$\begin{aligned} & \textbf{D}\textbf{C}\left( {\textbf{d}_{\textbf{i}},\textbf{d}_{\textbf{j}}} \right) = \frac{\sum \limits _{\textbf{a} = 1}^{\textbf{n}}{\textbf{d}_{\textbf{i},\textbf{a}}\textbf{d}_{\textbf{j},\textbf{a}}}}{\sqrt{\sum \limits _{\textbf{a} = 1}^{\textbf{n}}{\textbf{d}_{\textbf{i},\textbf{a}}}^{2}} \bullet \sqrt{\sum \limits _{\textbf{a} = 1}^{\textbf{n}}{\textbf{d}_{\textbf{j},\textbf{a}}}^{2}}} \end{aligned}$$
(5)
The element \(d_{i,a}\) and \(d_{j,a}\) represent the value in the a-th column in the row corresponding to drug \(d_{i}\) and \(d_{j}\) in matrix A.
After obtaining the drug similarity matrix DS, for any two drugs \(d_{i}\) and \(d_{j}\), if \(DS\left[{d_{i},d_{j}} \right]\) is within the top \(d_{rank}\%\) of all values in DS, they are considered to have a high similarity, meaning there is an edge between node \(d_{i}\) and node \(d_{j}\) in the Drug–Drug approximate network. Additionally, for the remaining unconnected nodes, the top \(d_{neighbor}\) nodes with the highest similarity are selected as their neighbor nodes, and corresponding edges are added. The resulting network constructed through this method is the D–D network.
Similarly, the similarity matrix between different targets is defined as TS. For any two targets \(t_{i}\) and \(t_{j}\) in the set T, we have:
$$\begin{aligned} \textbf{T}\textbf{S}\left[{\textbf{t}_{\textbf{i}},\textbf{t}_{\textbf{j}}} \right]= \frac{1 + \textbf{T}\textbf{R}\left( {\textbf{t}_{\textbf{i}},\textbf{t}_{\textbf{j}}} \right) }{2} \cdot \frac{1 + \textbf{T}\textbf{C}\left( {\textbf{t}_{\textbf{i}},\textbf{t}_{\textbf{j}}} \right) }{2} \end{aligned}$$
(6)
Where TR is the Pearson similarity and TC is the cosine similarity, calculated as follows:
$$\begin{aligned} & \textbf{T}\textbf{R}\left( {\textbf{t}_{\textbf{i}},\textbf{t}_{\textbf{j}}} \right) = \frac{\sum \limits _{\textbf{b} = 1}^{\textbf{m}}{\left( {\textbf{t}_{\textbf{i},\textbf{b}} – \overset{-}{\textbf{t}_{\textbf{i}}}} \right) \cdot \left( {\textbf{t}_{\textbf{j},\textbf{b}} – \overset{-}{\textbf{t}_{\textbf{j}}}} \right) }}{\sqrt{{\sum \limits _{\textbf{b} = 1}^{\textbf{m}}\left( {\textbf{t}_{\textbf{i},\textbf{b}} – \overset{-}{\textbf{t}_{\textbf{i}}}} \right) ^{2}} \cdot {\sum \limits _{\textbf{b} = 1}^{\textbf{m}}\left( {\textbf{t}_{\textbf{j},\textbf{b}} – \overset{-}{\textbf{t}_{\textbf{j}}}} \right) ^{2}}}} \end{aligned}$$
(7)
$$\begin{aligned} & \textbf{T}\textbf{C}\left( {\textbf{t}_{\textbf{i}},\textbf{t}_{\textbf{j}}} \right) = \frac{\sum \limits _{\textbf{b} = 1}^{\textbf{m}}{\textbf{t}_{\textbf{i},\textbf{b}}\textbf{t}_{\textbf{j},\textbf{b}}}}{\sqrt{\sum \limits _{\textbf{b} = 1}^{\textbf{m}}{\textbf{t}_{\textbf{i},\textbf{b}}}^{2}} \bullet \sqrt{\sum \limits _{\textbf{b} = 1}^{\textbf{m}}{\textbf{t}_{\textbf{j},\textbf{b}}}^{2}}} \end{aligned}$$
(8)
The element \(t_{i,b}\) and \(t_{j,b}\) represent the value in the b-th element of the column corresponding to target \(t_{i}\) and \(t_{j}\) in matrix A.
After obtaining the target similarity matrix TS, for any two targets \(t_{i}\) and \(t_{j}\), if \(TS\left[t_{i},t_{j} \right]\) is within the top \(t_{rank}\%\) of all values in TS, they are considered to have a high similarity, meaning there is an edge between node \(t_{i}\) and node \(t_{j}\) in the Target–Target approximate network. Additionally, for the remaining unconnected nodes, the top \(t_{neighbor}\) nodes with the highest similarity are selected as their neighbor nodes, and corresponding edges are added. The resulting network constructed through this method is the T–T network.
By merging the D–D network, T–T network, and the existing D–T network, the D–D–T–T network is obtained.
Graph encoder
The graph encoder is composed of multiple stacked GATConv layers, SAGEConv layers, and FC layers. Based on the topological relationships in the existing D–T network, it updates the corresponding node information through a “message passing” mechanism [35], as shown in Fig. 3A.
The drug and target feature vectors processed by the sequence attribute extractor have the same dimension, so they can be placed in the same graph neural network for processing. The D–D–T–T network is represented as \(G = (V,E)\), where V is the set of nodes, consisting of drug and target nodes, and E is the set of edges, each node \(v_{i}\) has a corresponding feature vector \(h_{i}\).
GATConv, proposed by Veličković et al. [36], aims to learn the importance of neighboring nodes and use the learned importance weights to perform a weighted sum, thereby updating the node itself. For any node \(v_{i}\), its feature vector in the \(l+1\) layer, \(h_{i}^{l+1}\), can be expressed as:
$$\begin{aligned} \textbf{h}_{\textbf{i}}^{\textbf{l} + 1} = {\sum \limits _{\textbf{j}\mathbf {\epsilon }\textbf{N}{(\textbf{i})}}{\mathbf {\alpha }_{\textbf{i}\textbf{j}}\textbf{W}^{\textbf{l}}\textbf{h}_{\textbf{j}}^{\textbf{l}}}} \end{aligned}$$
(9)
Where N(i) represents the neighboring nodes of node \(v_{i}\), \(W^{l}\) is the weight matrix of the l-th layer, and \(\alpha _{ij}\) is the importance weight of neighboring node \(v_{j}\) to node \(v_{i}\), which is calculated as follows:
$$\begin{aligned} & \mathbf {\alpha }_{\textbf{i}\textbf{j}}^{\textbf{l}} = \textbf{s}\textbf{o}\textbf{f}\textbf{t}\textbf{m}\textbf{a}\textbf{x}\left( \textbf{e}_{\textbf{i}\textbf{j}}^{\textbf{l}} \right) \end{aligned}$$
(10)
$$\begin{aligned} & \textbf{e}_{\textbf{i}\textbf{j}}^{\textbf{l}} = \textbf{L}\textbf{e}\textbf{a}\textbf{k}\textbf{y}\textbf{R}\textbf{e}\textbf{L}\textbf{U}\left( {\mathbf {\alpha }^{\textbf{T}}\left[{\textbf{W}\textbf{h}_{\textbf{i}}^{\textbf{l}} \parallel \textbf{W}\textbf{h}_{\textbf{j}}^{\textbf{l}}} \right]} \right) \end{aligned}$$
(11)
SAGEConv, proposed by Hamilton et al. [37], is designed for large-scale graph structures. Its core idea is to sample the neighboring nodes of a given node and aggregate the sampled neighbors using an aggregation function, thereby updating the node itself. For any node \(v_{i}\), its feature vector in the \(l+1\) layer, \(h^{l+1}\), can be expressed as:
$$\begin{aligned} \textbf{h}_{\textbf{i}}^{\textbf{l} + 1} = \mathbf {\sigma }\left( {\textbf{W}^{\textbf{l}}\left[{\textbf{h}_{\textbf{i}}^{\textbf{l}} \parallel \textbf{h}_{\textbf{N}{(\textbf{i})}}^{\textbf{l}}} \right]} \right) \end{aligned}$$
(12)
Where \(\sigma ()\) is the activation function, \(h_{N(i)}^{l}\) represents the aggregated features of the sampled neighboring nodes. The aggregation methods here are diverse, and the one we use is the mean aggregation, which is calculated as follows:
$$\begin{aligned} \textbf{h}_{\textbf{N}{(\textbf{i})}}^{\textbf{l}} = \frac{1}{\left| {\textbf{N}\left( \textbf{i} \right) } \right| }{\sum \limits _{\textbf{h}_{\textbf{i}}^{\textbf{l}}\mathbf {\epsilon }\textbf{N}{(\textbf{i})}}\textbf{h}_{\textbf{j}}^{\textbf{l}}} \end{aligned}$$
(13)
The graph encoder is updated based on a local iterative method, it relies on the existing graph structure. Therefore, before each round of training begins, it is necessary to determine whether each edge should be retained, i.e., the dynamic connection of graph nodes. Whether an edge is retained depends on the weight corresponding to that edge. All edge weights are between 0 and 1. If the weight of an edge is greater than 0.5, the edge is considered important and will be retained; otherwise, it will be discarded. If an edge is retained, the two endpoints of that edge will exchange information. Otherwise, each endpoint will only retain its own information. The edge update mechanism is illustrated in Fig. 3B.
Additionally, traditional graph neural networks may suffer from over-smoothing, where the differences between node features diminish as the network depth increases. To mitigate this, the original features from the previous layer are carried over into the new layer, helping to retain the original feature information more effectively. The node update mechanism is illustrated in Fig. 3C.
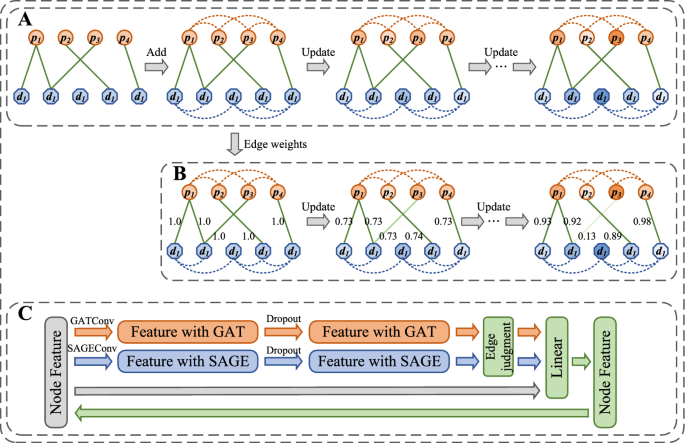
Node update in the graph encoder (A), edge update in the graph encoder (B), Update in each layer of graph encoder (C)
Graph decoder
The graph decoder can calculate the probability of a specific edge existing between nodes. Specifically, it computes the dot product of the feature vectors of the two endpoints of each edge and uses this result as the initial probability for that edge. Subsequently, all edge probability values are processed using the sigmoid function, and the processed results are treated as the probability of each edge’s existence, which corresponds to the likelihood of interaction between the drug node and the target node on that edge.